Implementing Solution to Multiple Traveling Salesman Problem

Assume you are a traveling salesman, selling coffee. You want to start from your home, sell coffee to costumers at different places and return to your home. You are intelligent and you want to minimize the distance you travel. The route you choose will be a solution to the traveling salesman problem.
How to solve?
Traveling Salesman Problem (TSP) is proven to be unsolvable in polynomial time, therefore lots of heuristic/meta-heuristic algorithms are used to solve that and give near optimal solutions. This link is parano’s genetic TSP solution. It is also available online.
Genetic Algorithm
If you are going to read the code mentioned above, it is good to know Genetic Algorithm and search for its methods inside the code.
- Population: in genetic algorithm, there is a pool of solutions, initialized randomly. Each solutions is called an individual, and the solution is coded inside it. In TSP, each individual is a rotating array of numbers, which shows a route between costumers. For example,
3 0 4 2 5 1means going from3to0, then4, then2and so on. Note that it also goes from1to3, because the list is rotating. Therefore, it is equivalent with for example2 5 1 3 0 4. - Initialization: random evaluation of the population is done here.
- Fitness function: since it is important to compare different solutions, a fitness functoin is defined. It accepts an individual and returns how much it feets. For TSP, it is defined as
evaluationmethod, which returns the sum of the distances between the costumers. However, since it returns smaller values for better solutions, the fitness is defined as1/evaluation, which returns higher values as the given solution (passed individual) gets better. - Crossover: combines two individuals and creates new one(s). It is one of the most important parts of a Genetic Algorithm solution, and there are several scientific papres proposing different crossovers for TSP. The one that is used in parano’s code, is a simple greedy algorithm which creates two children for each pair of parents. It starts from a random starting node (costumer), and add it to the child. Then it checks the next nodes after the starting node in both parents. Next node of the child will be selected from the parent in which the next node is closer to the starting node. For example, if starting node is
7, and the next nodes in parents are3and9respectively, ifdistance(7, 3) < distance(7, 9)then3will be selected, otherwise9will be the next node. The other child is found going to the previous node of the selected node, instead of going to the next. - Natural selection: or simply parent selection, selects a pair of fit parents from the population. They will be sent to crossover to create the new generation.
- Mutation: to search all of the solution space, the mutation is also happen to the population. It is done with low random probabilities such as 0.01. For TSP, again several different mutations are introduced. For example, swapping two random indices in the array, or reversing a random subset of the array in place. It is shown in the above image.
- Solve method: almost all of the previous methods are called in this method. It means that for a number of generations, we create new populations by using crossover and mutaion over best fit individuals. A semi-code for this method is as below:
function solve() {
let population = initialization();
for(let i = 0; i < generationCount; i++) {
let newPopulation = [];
for(let j = 0; j < population.size(); j+= 2) {
let parent1 = selectFitParent(population);
let parent2 = selectFitParent(population.filter(p => p != parent1));
let children = crossOver(parent1, parent2);
children[0] = mutate(children[0]);
children[1] = mutate(children[1]);
newPopulation.push(children[0]);
newPopulation.push(children[1]);
}
population = newPopulation;
}
}In the code repository, the for loop is replaced with a method called GANextGeneration, which is called using Javascript setInterval method.
More than one salesman…
Assume you are living with your friends or family, and they decide to help you. You all start from home, each travels to a different set of costumers and returns. The new problem you are facing is called Multiple Traveling Salesman Problem (MTSP).
It can be divided into two problems:
- Select destinations for each salesman,
- Solve TSP for each salesman.
However, there are some ways to convert MTSP to TSP, and apply the previously built solutions to the new problem.
Multiple salesmen? It is easy!
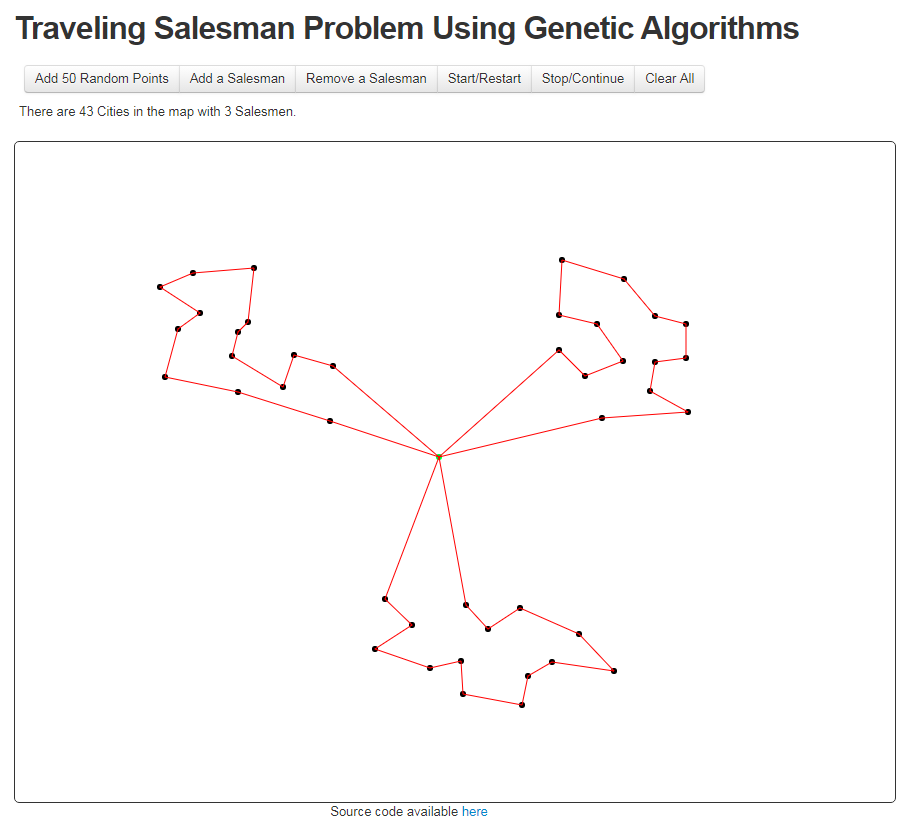
I changed parano’s solution, to work for Multiple TSP (MTSP), in which there are more than one traveling salesman. It is an online multiple traveling salesman problem solver. The source code is also available.
Two easy steps I took to change the base code from TSP to MTSP solver:
1. Added source nodes for each salesman
For TSP, we have only one source node. I added several other source nodes at the same place with the main source.
This way, one of the possible solutions for 10 nodes and two salesmen may be 3 8 4 0 5 7 1 9 0 6 2. Since the list is rotating, it can be read as 5 7 1 9 0 6 2 3 8 4 0. Different salesmen’s paths are separated with 0, which is the index of the source node.
However, we may end up paths with length 0, for example 1 7 4 8 0 0 3 5 2 9 6, in which one of the salesmen started from 0 and immediately went to 0.
To avoid this, the distance between source nodes is assumed to be infinity.
2. Changed the evaluation method to consider multiple salesman
Previous evaluation method was returning the sum of the distances. In other words, it was calculating the total distance the salesman travelled. In the code, it is implemented like this (of course after a for loop calculating it):
return sum;In order to maintain all of the salesmen’s travelled distances almost the same, I changed above code to this:
var L2 = sumForSalesman.reduce((t, x) => t + x*x, 0);
return L2 / sum;In above code, sumForSalesman is an array of the distance each salesman traveled. I square each of its members and calculate the sum of them. If there is only one salesman, the result will be the same as previous implementation. Therefore nothing is changed from the TSP solver perspective. However, when there are more than one salesman, above formula returns larger values for more unfair routes. For example, if we have two salesmen and they traveled 10 KM in total, the result will be different for this cases:
- both traveled 4 KM:
(4*4 + 4*4) / 8which gives4 - one traveled 5 KM and the other 3 KM:
(5*5 + 3*3) / 8which gives4.25 - one traveled 1 KM and the other 7 KM:
(1*1 + 7*7) / 8which gives6.25
If you think this policy won’t give the opimum solution every time, you are right! Here is an example, for the same path, 2+6 and 5+5 solutions are prefered over 1+6, although the sum for the last is smaller than those two.
Conclusion
There are lots of interesting problems to solve with regards Traveling Salesman Problem. For example, consider the salesmen are not bound to start and end from the same location, or some of them have constraints to visit a certain number of nodes (costumers), or travel a certain distance at most. In addition, several other crossover and mutation methods may be tested to help the method to find an acceptable answer earlier.